The Mersenne Twister is a twisted generalized feedback shift-register generator of Matsumoto and Nishimura. The period of this generator is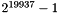 
and it is equi-distributed in 623 dimensions for 32-bit numbers. The time performance of this generator is comparable to the commonly used generators.
This implementation is specialized for both 32-bit and 64-bit architectures. The generators differ sligthly in the initialization and generation phase so they produce two completly different sequences.
The generator gives back random numbers of serveral types. To get a random number from a range of a floating point type you can use one form of the operator() or the real() member function. If you want to get random number from the {0, 1, ..., n-1} integer range use the operator[] or the integer() method. And to get random number from the whole range of an integer type you can use the argumentless integer() or uinteger() functions. After all you can get random bool with equal chance of true and false or given probability of true result with the boolean() member functions.
// The commented code is identical to the other double a = rnd(); // [0.0, 1.0) // double a = rnd.real(); // [0.0, 1.0) double b = rnd(100.0); // [0.0, 100.0) // double b = rnd.real(100.0); // [0.0, 100.0) double c = rnd(1.0, 2.0); // [1.0, 2.0) // double c = rnd.real(1.0, 2.0); // [1.0, 2.0) int d = rnd[100000]; // 0..99999 // int d = rnd.integer(100000); // 0..99999 int e = rnd[6] + 1; // 1..6 // int e = rnd.integer(1, 1 + 6); // 1..6 int b = rnd.uinteger<int>(); // 0 .. 2^31 - 1 int c = rnd.integer<int>(); // - 2^31 .. 2^31 - 1 bool g = rnd.boolean(); // P(g = true) = 0.5 bool h = rnd.boolean(0.8); // P(h = true) = 0.8
LEMON provides a global instance of the random number generator which name is rnd. Usually it is a good programming convenience to use this global generator to get random numbers.
#include <lemon/random.h>
Public Member Functions | |
Initialization | |
| Random () | |
| Default constructor. | |
| template<typename Number > | |
| Random (Number seed) | |
| Constructor with seed. | |
| template<typename Iterator > | |
| Random (Iterator begin, Iterator end) | |
| Constructor with array seeding. | |
| Random (const Random &other) | |
| Copy constructor. | |
| Random & | operator= (const Random &other) |
| Assign operator. | |
| template<typename Number > | |
| void | seed (Number seed) |
| Seeding random sequence. | |
| template<typename Iterator > | |
| void | seed (Iterator begin, Iterator end) |
| Seeding random sequence. | |
| bool | seed () |
| Seeding from file or from process id and time. | |
| bool | seedFromFile (const std::string &file="/dev/urandom", int offset=0) |
| Seeding from file. | |
| bool | seedFromTime () |
| Seding from process id and time. | |
Uniform Distributions | |
| template<typename Number > | |
| Number | real () |
| Returns a random real number from the range [0, 1) | |
| double | real () |
| double | operator() () |
| Returns a random real number from the range [0, 1) | |
| double | operator() (double b) |
| Returns a random real number from the range [0, b) | |
| double | operator() (double a, double b) |
| Returns a random real number from the range [a, b) | |
| template<typename Number > | |
| Number | integer (Number b) |
| Returns a random integer from a range. | |
| template<typename Number > | |
| Number | integer (Number a, Number b) |
| Returns a random integer from a range. | |
| template<typename Number > | |
| Number | operator[] (Number b) |
| Returns a random integer from a range. | |
| template<typename Number > | |
| Number | uinteger () |
| Returns a random non-negative integer. | |
| unsigned int | uinteger () |
| template<typename Number > | |
| Number | integer () |
| Returns a random integer. | |
| int | integer () |
| bool | boolean () |
| Returns a random bool. | |
Non-uniform Distributions | |
| bool | boolean (double p) |
| Returns a random bool with given probability of true result. | |
| double | gauss () |
| Standard normal (Gauss) distribution. | |
| double | gauss (double mean, double std_dev) |
| Normal (Gauss) distribution with given mean and standard deviation. | |
| double | lognormal (double n_mean, double n_std_dev) |
| Lognormal distribution. | |
| double | lognormal (const std::pair< double, double > ¶ms) |
| Lognormal distribution. | |
| std::pair< double, double > | lognormalParamsFromMD (double mean, double std_dev) |
| Compute the lognormal parameters from mean and standard deviation. | |
| double | lognormalMD (double mean, double std_dev) |
| double | exponential (double lambda=1.0) |
| Exponential distribution with given mean. | |
| double | gamma (int k) |
| Gamma distribution with given integer shape. | |
| double | gamma (double k, double theta=1.0) |
| Gamma distribution with given shape and scale parameter. | |
| double | weibull (double k, double lambda) |
| Weibull distribution. | |
| double | pareto (double k, double x_min) |
| Pareto distribution. | |
| int | poisson (double lambda) |
| Poisson distribution. | |
Two Dimensional Distributions | |
| dim2::Point< double > | disc () |
| dim2::Point< double > | gauss2 () |
| A kind of two dimensional normal (Gauss) distribution. | |
| dim2::Point< double > | exponential2 () |
| A kind of two dimensional exponential distribution. | |
| Random | ( | ) | [inline] |
Constructor with constant seeding.
| Random | ( | Number | seed | ) | [inline] |
Constructor with seed. The current number type will be converted to the architecture word type.
| Random | ( | Iterator | begin, |
| Iterator | end | ||
| ) | [inline] |
Constructor with array seeding. The given range should contain any number type and the numbers will be converted to the architecture word type.
Copy constructor. The generated sequence will be identical to the other sequence. It can be used to save the current state of the generator and later use it to generate the same sequence.
Assign operator. The generated sequence will be identical to the other sequence. It can be used to save the current state of the generator and later use it to generate the same sequence.
| void seed | ( | Number | seed | ) | [inline] |
Seeding the random sequence. The current number type will be converted to the architecture word type.
| void seed | ( | Iterator | begin, |
| Iterator | end | ||
| ) | [inline] |
Seeding the random sequence. The given range should contain any number type and the numbers will be converted to the architecture word type.
| bool seed | ( | ) | [inline] |
By default, this function calls the seedFromFile() member function with the /dev/urandom file. If it does not success, it uses the seedFromTime().
true. | bool seedFromFile | ( | const std::string & | file = "/dev/urandom", |
| int | offset = 0 |
||
| ) | [inline] |
Seeding the random sequence from file. The linux kernel has two devices, /dev/random and /dev/urandom which could give good seed values for pseudo random generators (The difference between two devices is that the random may block the reading operation while the kernel can give good source of randomness, while the urandom does not block the input, but it could give back bytes with worse entropy).
| file | The source file |
| offset | The offset, from the file read. |
true when the seeding successes. | bool seedFromTime | ( | ) | [inline] |
Seding from process id and time. This function uses the current process id and the current time for initialize the random sequence.
true. | Number real | ( | ) | [inline] |
It returns a random real number from the range [0, 1). The default Number type is double.
| double operator() | ( | ) | [inline] |
It returns a random double from the range [0, 1).
| double operator() | ( | double | b | ) | [inline] |
It returns a random real number from the range [0, b).
| double operator() | ( | double | a, |
| double | b | ||
| ) | [inline] |
It returns a random real number from the range [a, b).
| Number integer | ( | Number | b | ) | [inline] |
It returns a random integer from the range {0, 1, ..., b - 1}.
| Number integer | ( | Number | a, |
| Number | b | ||
| ) | [inline] |
It returns a random integer from the range {a, a + 1, ..., b - 1}.
| Number operator[] | ( | Number | b | ) | [inline] |
It returns a random integer from the range {0, 1, ..., b - 1}.
| Number uinteger | ( | ) | [inline] |
It returns a random non-negative integer uniformly from the whole range of the current Number type. The default result type of this function is unsigned int.
| Number integer | ( | ) | [inline] |
It returns a random integer uniformly from the whole range of the current Number type. The default result type of this function is int.
| bool boolean | ( | ) | [inline] |
It returns a random bool. The generator holds a buffer for random bits. Every time when it become empty the generator makes a new random word and fill the buffer up.
| bool boolean | ( | double | p | ) | [inline] |
It returns a random bool with given probability of true result.
| double gauss | ( | ) | [inline] |
Standard normal (Gauss) distribution.
| double gauss | ( | double | mean, |
| double | std_dev | ||
| ) | [inline] |
Normal (Gauss) distribution with given mean and standard deviation.
| double lognormal | ( | double | n_mean, |
| double | n_std_dev | ||
| ) | [inline] |
Lognormal distribution. The parameters are the mean and the standard deviation of exp(X).
| double lognormal | ( | const std::pair< double, double > & | params | ) | [inline] |
Lognormal distribution. The parameter is an std::pair of the mean and the standard deviation of exp(X).
| std::pair<double,double> lognormalParamsFromMD | ( | double | mean, |
| double | std_dev | ||
| ) | [inline] |
This function computes the lognormal parameters from mean and standard deviation. The return value can direcly be passed to lognormal().
| double lognormalMD | ( | double | mean, |
| double | std_dev | ||
| ) | [inline] |
Lognormal distribution with given mean and standard deviation.
| double exponential | ( | double | lambda = 1.0 | ) | [inline] |
This function generates an exponential distribution random number with mean 1/lambda.
| double gamma | ( | int | k | ) | [inline] |
This function generates a gamma distribution random number.
| k | shape parameter (k>0 integer) |
| double gamma | ( | double | k, |
| double | theta = 1.0 |
||
| ) | [inline] |
This function generates a gamma distribution random number.
| k | shape parameter (k>0) |
| theta | scale parameter |
| double weibull | ( | double | k, |
| double | lambda | ||
| ) | [inline] |
This function generates a Weibull distribution random number.
| k | shape parameter (k>0) |
| lambda | scale parameter (lambda>0) |
| double pareto | ( | double | k, |
| double | x_min | ||
| ) | [inline] |
This function generates a Pareto distribution random number.
| k | shape parameter (k>0) |
| x_min | location parameter (x_min>0) |
| int poisson | ( | double | lambda | ) | [inline] |
This function generates a Poisson distribution random number with parameter lambda.
The probability mass function of this distribusion is
![\[ \frac{e^{-\lambda}\lambda^k}{k!} \]](form_89.png)
| dim2::Point<double> disc | ( | ) | [inline] |
Uniform distribution on the full unit circle.
| dim2::Point<double> gauss2 | ( | ) | [inline] |
This function provides a turning symmetric two-dimensional distribution. Both coordinates are of standard normal distribution, but they are not independent.
| dim2::Point<double> exponential2 | ( | ) | [inline] |
This function provides a turning symmetric two-dimensional distribution. The x-coordinate is of conditionally exponential distribution with the condition that x is positive and y=0. If x is negative and y=0 then, -x is of exponential distribution. The same is true for the y-coordinate.
1.7.3