Maximum Flow Algorithms

Detailed Description

This group contains the algorithms for finding maximum flows and feasible circulations.

The maximum flow problem is to find a flow of maximum value between a single source and a single target. Formally, there is a 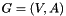$G=(V,A)$ digraph, a 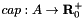$cap: A\rightarrow\mathbf{R}^+_0$ capacity function and 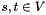$s, t \in V$ source and target nodes. A maximum flow is an 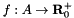$f: A\rightarrow\mathbf{R}^+_0$ solution of the following optimization problem.

$\max\sum_{sv\in A} f(sv) - \sum_{vs\in A} f(vs)$

$\sum_{uv\in A} f(uv) = \sum_{vu\in A} f(vu) \quad \forall u\in V\setminus\{s,t\}$

$0 \leq f(uv) \leq cap(uv) \quad \forall uv\in A$

Preflow implements the preflow push-relabel algorithm of Goldberg and Tarjan for solving this problem. It also provides functions to query the minimum cut, which is the dual problem of maximum flow.

Circulation is a preflow push-relabel algorithm implemented directly for finding feasible circulations, which is a somewhat different problem, but it is strongly related to maximum flow. For more information, see Circulation.

Classes
class	Circulation< GR, LM, UM, SM, TR >
	Push-relabel algorithm for the network circulation problem. More...
class	Preflow< GR, CAP, TR >
	Preflow algorithm class. More...
Files
file	circulation.h
	Push-relabel algorithm for finding a feasible circulation.
file	preflow.h
	Implementation of the preflow algorithm.

Maximum Flow Algorithms

Detailed Description

Classes

Files