Circulation< GR, LM, UM, SM, TR > Class Template Reference

---

Detailed Description

template<typename GR, typename LM, typename UM, typename SM, typename TR>
class lemon::Circulation< GR, LM, UM, SM, TR >

This class implements a push-relabel algorithm for the network circulation problem. It is to find a feasible circulation when lower and upper bounds are given for the flow values on the arcs and lower bounds are given for the difference between the outgoing and incoming flow at the nodes.

The exact formulation of this problem is the following. Let 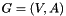be a digraph,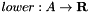 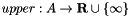denote the lower and upper bounds on the arcs, for which 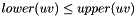holds for all 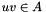, and 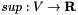denotes the signed supply values of the nodes. If 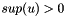, then 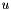is a supply node with 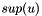supply, if 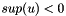, then 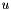is a demand node with 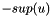demand. A feasible circulation is an 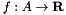solution of the following problem.

The sum of the supply values, i.e. 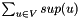must be zero or negative in order to have a feasible solution (since the sum of the expressions on the left-hand side of the inequalities is zero). It means that the total demand must be greater or equal to the total supply and all the supplies have to be carried out from the supply nodes, but there could be demands that are not satisfied. If 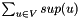is zero, then all the supply/demand constraints have to be satisfied with equality, i.e. all demands have to be satisfied and all supplies have to be used.

If you need the opposite inequalities in the supply/demand constraints (i.e. the total demand is less than the total supply and all the demands have to be satisfied while there could be supplies that are not used), then you could easily transform the problem to the above form by reversing the direction of the arcs and taking the negative of the supply values (e.g. using ReverseDigraph and NegMap adaptors).

This algorithm either calculates a feasible circulation, or provides a barrier, which prooves that a feasible soultion cannot exist.

Note that this algorithm also provides a feasible solution for the minimum cost flow problem.

Template Parameters:

GR	The type of the digraph the algorithm runs on.
LM	The type of the lower bound map. The default map type is GR::ArcMap<int>.
UM	The type of the upper bound (capacity) map. The default map type is LM.
SM	The type of the supply map. The default map type is GR::NodeMap<UM::Value>.

#include <lemon/circulation.h>

List of all members.

Classes
struct	SetElevator
	Named parameter for setting Elevator type More...
struct	SetFlowMap
	Named parameter for setting FlowMap type More...
struct	SetStandardElevator
	Named parameter for setting Elevator type with automatic allocation More...
Public Types
typedef TR	Traits
	The traits class of the algorithm.
typedef Traits::Digraph	Digraph
	The type of the digraph the algorithm runs on.
typedef Traits::Value	Value
	The type of the flow and supply values.
typedef Traits::LowerMap	LowerMap
	The type of the lower bound map.
typedef Traits::UpperMap	UpperMap
	The type of the upper bound (capacity) map.
typedef Traits::SupplyMap	SupplyMap
	The type of the supply map.
typedef Traits::FlowMap	FlowMap
	The type of the flow map.
typedef Traits::Elevator	Elevator
	The type of the elevator.
typedef Traits::Tolerance	Tolerance
	The type of the tolerance.
Public Member Functions
	Circulation (const Digraph &graph, const LowerMap &lower, const UpperMap &upper, const SupplyMap &supply)
	Constructor.
	~Circulation ()
	Destructor.
Circulation &	lowerMap (const LowerMap &map)
	Sets the lower bound map.
Circulation &	upperMap (const UpperMap &map)
	Sets the upper bound (capacity) map.
Circulation &	supplyMap (const SupplyMap &map)
	Sets the supply map.
Circulation &	flowMap (FlowMap &map)
	Sets the flow map.
Circulation &	elevator (Elevator &elevator)
	Sets the elevator used by algorithm.
const Elevator &	elevator () const
	Returns a const reference to the elevator.
Circulation &	tolerance (const Tolerance &tolerance)
const Tolerance &	tolerance () const
Execution Control
The simplest way to execute the algorithm is to call run(). If you need more control on the initial solution or the execution, first you have to call one of the init() functions, then the start() function.
void	init ()
	Initializes the internal data structures.
void	greedyInit ()
	Initializes the internal data structures using a greedy approach.
bool	start ()
	Executes the algorithm.
bool	run ()
	Runs the algorithm.
Query Functions
The results of the circulation algorithm can be obtained using these functions. Either run() or start() should be called before using them.
Value	flow (const Arc &arc) const
	Returns the flow value on the given arc.
const FlowMap &	flowMap () const
	Returns a const reference to the flow map.
bool	barrier (const Node &node) const
	Returns true if the given node is in a barrier.
template<class BarrierMap >
void	barrierMap (BarrierMap &bar) const
	Gives back a barrier.
Checker Functions
The feasibility of the results can be checked using these functions. Either run() or start() should be called before using them.
bool	checkFlow () const
	Check if the found flow is a feasible circulation.
bool	checkBarrier () const
	Check whether or not the last execution provides a barrier.

---

Constructor & Destructor Documentation

Circulation	(	const Digraph &	graph,
		const LowerMap &	lower,
		const UpperMap &	upper,
		const SupplyMap &	supply
	)		[inline]

The constructor of the class.

Parameters:

graph	The digraph the algorithm runs on.
lower	The lower bounds for the flow values on the arcs.
upper	The upper bounds (capacities) for the flow values on the arcs.
supply	The signed supply values of the nodes.

---

Member Function Documentation

Circulation& lowerMap

(

const LowerMap &

map

)

[inline]

Sets the lower bound map.

Returns:

(*this)

Circulation& upperMap

(

const UpperMap &

map

)

[inline]

Sets the upper bound (capacity) map.

Returns:

(*this)

Circulation& supplyMap

(

const SupplyMap &

map

)

[inline]

Sets the supply map.

Returns:

(*this)

Circulation& flowMap

(

FlowMap &

map

)

[inline]

Sets the flow map. If you don't use this function before calling run() or init(), an instance will be allocated automatically. The destructor deallocates this automatically allocated map, of course.

Returns:

(*this)

Circulation& elevator

(

Elevator &

elevator

)

[inline]

Sets the elevator used by algorithm. If you don't use this function before calling run() or init(), an instance will be allocated automatically. The destructor deallocates this automatically allocated elevator, of course.

Returns:

(*this)

const Elevator& elevator

(

)

const [inline]

Returns a const reference to the elevator.

Precondition:

Either run() or init() must be called before using this function.

Circulation& tolerance

(

const Tolerance &

tolerance

)

[inline]

Sets the tolerance used by algorithm.

const Tolerance& tolerance

(

)

const [inline]

Returns a const reference to the tolerance.

void init

(

)

[inline]

Initializes the internal data structures and sets all flow values to the lower bound.

void greedyInit

(

)

[inline]

Initializes the internal data structures using a greedy approach to construct the initial solution.

bool start

(

)

[inline]

This function executes the algorithm.

Returns:

true if a feasible circulation is found.

See also:

barrier()

barrierMap()

bool run

(

)

[inline]

This function runs the algorithm.

Returns:

true if a feasible circulation is found.

Note:

Apart from the return value, c.run() is just a shortcut of the following code.

   c.greedyInit();
   c.start();

Value flow

(

const Arc &

arc

)

const [inline]

Returns the flow value on the given arc.

Precondition:

Either run() or init() must be called before using this function.

const FlowMap& flowMap

(

)

const [inline]

Returns a const reference to the arc map storing the found flow.

Precondition:

Either run() or init() must be called before using this function.

bool barrier

(

const Node &

node

)

const [inline]

Barrier is a set B of nodes for which

holds. The existence of a set with this property prooves that a feasible circualtion cannot exist.

This function returns true if the given node is in the found barrier. If a feasible circulation is found, the function gives back false for every node.

Precondition:

Either run() or init() must be called before using this function.

See also:

barrierMap()

checkBarrier()

void barrierMap

(

BarrierMap &

bar

)

const [inline]

This function sets bar to the characteristic vector of the found barrier. bar should be a writable node map with bool (or convertible) value type.

If a feasible circulation is found, the function gives back an empty set, so bar[v] will be false for all nodes v.

Note:

This function calls barrier() for each node, so it runs in O(n) time.

Precondition:

Either run() or init() must be called before using this function.

See also:

barrier()

checkBarrier()

bool checkFlow

(

)

const [inline]

Check if the found flow is a feasible circulation,

bool checkBarrier

(

)

const [inline]

Check whether or not the last execution provides a barrier.

See also:

barrier()

barrierMap()