MaxWeightedPerfectMatching< GR, WM > Class Template Reference

---

Detailed Description

template<typename GR, typename WM>
class lemon::MaxWeightedPerfectMatching< GR, WM >

This class provides an efficient implementation of Edmond's maximum weighted perfect matching algorithm. The implementation is based on extensive use of priority queues and provides time complexity.

The maximum weighted perfect matching problem is to find a subset of the edges in an undirected graph with maximum overall weight for which each node has exactly one incident edge. It can be formulated with the following linear program.

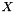where is the set of edges incident to a node in , is the set of edges with both ends in 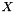and is the set of odd cardinality subsets of the nodes.

The algorithm calculates an optimal matching and a proof of the optimality. The solution of the dual problem can be used to check the result of the algorithm. The dual linear problem is the following.

The algorithm can be executed with the run() function. After it the matching (the primal solution) and the dual solution can be obtained using the query functions and the BlossomIt nested class, which is able to iterate on the nodes of a blossom. If the value type is integer, then the dual solution is multiplied by 4.

Template Parameters:

GR	The undirected graph type the algorithm runs on.
WM	The type edge weight map. The default type is GR::EdgeMap<int>.

#include <lemon/matching.h>

List of all members.

Classes
class	BlossomIt
	Iterator for obtaining the nodes of a blossom. More...
Public Types
typedef GR	Graph
	The graph type of the algorithm.
typedef WM	WeightMap
	The type of the edge weight map.
typedef WeightMap::Value	Value
	The value type of the edge weights.
typedef Graph::template NodeMap< typename Graph::Arc >	MatchingMap
	The type of the matching map.
Public Member Functions
	MaxWeightedPerfectMatching (const Graph &graph, const WeightMap &weight)
Execution Control
The simplest way to execute the algorithm is to use the run() member function.
void	init ()
	Initialize the algorithm.
void	fractionalInit ()
	Initialize the algorithm with fractional matching.
bool	start ()
	Start the algorithm.
bool	run ()
	Run the algorithm.
Primal Solution
Functions to get the primal solution, i.e. the maximum weighted perfect matching. Either run() or start() function should be called before using them.
Value	matchingWeight () const
	Return the weight of the matching.
bool	matching (const Edge &edge) const
	Return true if the given edge is in the matching.
Arc	matching (const Node &node) const
	Return the matching arc (or edge) incident to the given node.
const MatchingMap &	matchingMap () const
	Return a const reference to the matching map.
Node	mate (const Node &node) const
	Return the mate of the given node.
Dual Solution
Functions to get the dual solution. Either run() or start() function should be called before using them.
Value	dualValue () const
	Return the value of the dual solution.
Value	nodeValue (const Node &n) const
	Return the dual value (potential) of the given node.
int	blossomNum () const
	Return the number of the blossoms in the basis.
int	blossomSize (int k) const
	Return the number of the nodes in the given blossom.
Value	blossomValue (int k) const
	Return the dual value (ptential) of the given blossom.
Static Public Attributes
static const int	dualScale
	Scaling factor for dual solution.

---

Constructor & Destructor Documentation

MaxWeightedPerfectMatching	(	const Graph &	graph,
		const WeightMap &	weight
	)		[inline]

Constructor.

---

Member Function Documentation

void init

(

)

[inline]

This function initializes the algorithm.

void fractionalInit

(

)

[inline]

This function initializes the algorithm with a fractional matching. This initialization is also called jumpstart heuristic.

bool start

(

)

[inline]

This function starts the algorithm.

Precondition:

init() or fractionalInit() must be called before using this function.

bool run

(

)

[inline]

This method runs the MaxWeightedPerfectMatching algorithm.

Note:

mwpm.run() is just a shortcut of the following code.

   mwpm.fractionalInit();
   mwpm.start();

Value matchingWeight

(

)

const [inline]

This function returns the weight of the found matching.

Precondition:

Either run() or start() must be called before using this function.

bool matching

(

const Edge &

edge

)

const [inline]

This function returns true if the given edge is in the found matching.

Precondition:

Either run() or start() must be called before using this function.

Arc matching

(

const Node &

node

)

const [inline]

This function returns the matching arc (or edge) incident to the given node in the found matching or INVALID if the node is not covered by the matching.

Precondition:

Either run() or start() must be called before using this function.

const MatchingMap& matchingMap

(

)

const [inline]

This function returns a const reference to a node map that stores the matching arc (or edge) incident to each node.

Node mate

(

const Node &

node

)

const [inline]

This function returns the mate of the given node in the found matching or INVALID if the node is not covered by the matching.

Precondition:

Either run() or start() must be called before using this function.

Value dualValue

(

)

const [inline]

This function returns the value of the dual solution. It should be equal to the primal value scaled by dual scale.

Precondition:

Either run() or start() must be called before using this function.

Value nodeValue

(

const Node &

n

)

const [inline]

This function returns the dual value (potential) of the given node.

Precondition:

Either run() or start() must be called before using this function.

int blossomNum

(

)

const [inline]

This function returns the number of the blossoms in the basis.

Precondition:

Either run() or start() must be called before using this function.

See also:

BlossomIt

int blossomSize

(

int

k

)

const [inline]

This function returns the number of the nodes in the given blossom.

Precondition:

Either run() or start() must be called before using this function.

See also:

BlossomIt

Value blossomValue

(

int

k

)

const [inline]

This function returns the dual value (ptential) of the given blossom.

Precondition:

Either run() or start() must be called before using this function.

---

Member Data Documentation

const int dualScale [static]

Initial value:

      std::numeric_limits<Value>::is_integer ? 4 : 1

Scaling factor for dual solution, it is equal to 4 or 1 according to the value type.