Minimum Mean Cycle Algorithms

Detailed Description

This group contains the algorithms for finding minimum mean cycles [1], [21].

The minimum mean cycle problem is to find a directed cycle of minimum mean length (cost) in a digraph. The mean length of a cycle is the average length of its arcs, i.e. the ratio between the total length of the cycle and the number of arcs on it.

This problem has an important connection to conservative length functions, too. A length function on the arcs of a digraph is called conservative if and only if there is no directed cycle of negative total length. For an arbitrary length function, the negative of the minimum cycle mean is the smallest 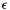value so that increasing the arc lengths uniformly by 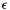results in a conservative length function.

LEMON contains three algorithms for solving the minimum mean cycle problem:

• KarpMmc Karp's original algorithm [21].
• HartmannOrlinMmc Hartmann-Orlin's algorithm, which is an improved version of Karp's algorithm [20].
• HowardMmc Howard's policy iteration algorithm [9], [10].

In practice, the Howard algorithm turned out to be by far the most efficient one, though the best known theoretical bound on its running time is exponential. Both Karp and Hartmann-Orlin algorithms run in time O(nm) and use space O(n²+m).

Classes
class	HartmannOrlinMmc< GR, CM, TR >
	Implementation of the Hartmann-Orlin algorithm for finding a minimum mean cycle. More...
class	HowardMmc< GR, CM, TR >
	Implementation of Howard's algorithm for finding a minimum mean cycle. More...
class	KarpMmc< GR, CM, TR >
	Implementation of Karp's algorithm for finding a minimum mean cycle. More...

Files
file	hartmann_orlin_mmc.h
	Hartmann-Orlin's algorithm for finding a minimum mean cycle.
file	howard_mmc.h
	Howard's algorithm for finding a minimum mean cycle.
file	karp_mmc.h
	Karp's algorithm for finding a minimum mean cycle.