7 Maps

Todo:

This page is under construction.

Todo:

The following contents are ported from the LEMON 0.x tutorial, thus they have to be thoroughly revised and reworked.

Warning

Currently, this section may contain old or faulty contents.

The LEMON maps are not only just storage classes, but also they are concepts of any key–value based data access. Beside the standard digraph maps, LEMON contains several "lightweight" map adaptor classes, which perform various operations on the data of the adapted maps when their access operations are called, but without actually copying or modifying the original storage. These classes also conform to the map concepts, thus they can be used like standard LEMON maps.

Maps play a central role in LEMON. As their name suggests, they map a certain range of keys to certain values. Each map has two typedef's to determine the types of keys and values, like this:

typedef Arc Key;
typedef double Value;

A map can be readable (ReadMap, for short), writable (WriteMap) or both (ReadWriteMap). There also exists a special type of ReadWrite map called reference map. In addition that you can read and write the values of a key, a reference map can also give you a reference to the value belonging to a key, so you have a direct access to the memory address where it is stored.

Each digraph structure in LEMON provides two standard map templates called ArcMap and NodeMap. Both are reference maps and you can easily assign data to the nodes and to the arcs of the digraph. For example if you have a digraph g defined as

ListDigraph g;

and you want to assign a floating point value to each arc, you can do it like this.

ListDigraph::ArcMap<double> length(g);

Note that you must give the underlying digraph to the constructor.

The value of a readable map can be obtained by operator[].

d=length[e];

where e is an instance of ListDigraph::Arc. (Or anything else that converts to ListDigraph::Arc, like ListDigraph::ArcIt or ListDigraph::OutArcIt etc.)

There are two ways to assign a new value to a key

• In case of a reference map operator[] gives you a reference to the value, thus you can use this.

  length[e]=3.5;

• Writable maps have a member function set(Key,const Value &) for this purpose.

  length.set(e,3.5);

The first case is more comfortable and if you store complex structures in your map, it might be more efficient. However, there are writable but not reference maps, so if you want to write a generic algorithm, you should insist on the second way.

How to Write Your Own Maps

Readable Maps

Readable maps are very frequently used as the input of an algorithm. For this purpose the most straightforward way is the use of the default maps provided by LEMON's digraph structures. Very often however, it is more convenient and/or more efficient to write your own readable map.

You can find some examples below. In these examples Digraph is the type of the particular digraph structure you use.

This simple map assigns 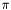to each arc.

struct MyMap 
{
  typedef double Value;
  typedef Digraph::Arc Key;
  double operator[](Key e) const { return PI;}
};

An alternative way to define maps is to use MapBase

struct MyMap : public MapBase<Digraph::Arc,double>
{
  Value operator[](Key e) const { return PI;}
};

Here is a bit more complex example. It provides a length function obtained from a base length function shifted by a potential difference.

class ReducedLengthMap  : public MapBase<Digraph::Arc,double>
{
  const Digraph &g;
  const Digraph::ArcMap<double> &orig_len;
  const Digraph::NodeMap<double> &pot;
  
public:
  Value operator[](Key e) const {
    return orig_len[e]-(pot[g.target(e)]-pot[g.source(e)]);
  }
  
  ReducedLengthMap(const Digraph &_g,
                   const Digraph::ArcMap &_o,
                   const Digraph::NodeMap &_p)
    : g(_g), orig_len(_o), pot(_p) {};
};

Then, you can call e.g. Dijkstra algoritm on this map like this:

...
ReducedLengthMap rm(g,len,pot);
Dijkstra<Digraph,ReducedLengthMap> dij(g,rm);
dij.run(s);
...

In the previous section we discussed digraph topology. That is the skeleton a complex digraph represented data-set needs. But how to assign the data itself to that skeleton?
Here come the maps in.

Introduction to maps

Maps play a central role in LEMON. As their name suggests, they map a certain range of keys to certain values. In LEMON there is many types of maps. Each map has two typedef's to determine the types of keys and values, like this:

typedef Arc Key;
typedef double Value;

(Except matrix maps, they have two key types.)

To make easy to use them - especially as template parameters - there are map concepts like by digraph classes.

• ReadMap - values can be read out with the operator[].

  value_typed_variable = map_instance[key_value]; 

• WriteMap - values can be set with the set() member function.

  map_instance.set(key_value, value_typed_expression); 

• ReadWriteMap - it's just a shortcut to indicate that the map is both readable and writable. It is delivered from them.
• ReferenceMap - a subclass of ReadWriteMap. It has two additional typedefs Reference and ConstReference and two overloads of operator[] to providing you constant or non-constant reference to the value belonging to a key, so you have a direct access to the memory address where it is stored.
• And there are the Matrix version of these maps, where the values are assigned to a pair of keys. The keys can be different types. (ReadMatrixMap, WriteMatrixMap, ReadWriteMatrixMap, ReferenceMatrixMap)

Digraphs' maps

Every mappable digraph class has two public templates: NodeMap<VALUE> and ArcMap<VALUE> satisfying the DigraphMap concept. If you want to assign data to nodes, just declare a NodeMap with the corresponding type. As an example, think of a arc-weighted digraph.

ListDigraph::ArcMap<int>  weight(digraph); 

You can see that the map needs the digraph whose arcs will mapped, but nothing more.

If the digraph class is extendable or erasable the map will automatically follow the changes you make. If a new node is added a default value is mapped to it. You can define the default value by passing a second argument to the map's constructor.

ListDigraph::ArcMap<int>  weight(digraph, 13); 

But keep in mind that VALUE has to have copy constructor.

Of course VALUE can be a rather complex type.

For practice let's see the following template function (from maps-summary.cc in the demo directory)!

The task is simple. We need the summary of some kind of data assigned to a digraph's nodes. (Whit a little trick the summary can be calculated only to a sub-digraph without changing this code. See SubDigraph techniques - that's LEMON's true potential.)

And the usage is simpler than the declaration suggests. The compiler deduces the template specialization, so the usage is like a simple function call.

Most of the time you will probably use digraph maps, but keep in mind, that in LEMON maps are more general and can be used widely.

If you want some 'real-life' examples see the next page, where we discuss algorithms (coming soon) and will use maps hardly. Or if you want to know more about maps read these advanced map techniques.

Here we discuss some advanced map techniques. Like writing your own maps or how to extend/modify a maps functionality with adaptors.

Writing Custom ReadMap

Readable Maps

Readable maps are very frequently used as the input of an algorithm. For this purpose the most straightforward way is the use of the default maps provided by LEMON's digraph structures. Very often however, it is more convenient and/or more efficient to write your own readable map.

You can find some examples below. In these examples Digraph is the type of the particular digraph structure you use.

This simple map assigns 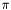to each arc.

struct MyMap 
{
  typedef double Value;
  typedef Digraph::Arc Key;
  double operator[](const Key &e) const { return PI;}
};

An alternative way to define maps is to use MapBase

struct MyMap : public MapBase<Digraph::Arc,double>
{
  Value operator[](const Key& e) const { return PI;}
};

Here is a bit more complex example. It provides a length function obtained from a base length function shifted by a potential difference.

class ReducedLengthMap  : public MapBase<Digraph::Arc,double>
{
  const Digraph &g;
  const Digraph::ArcMap<double> &orig_len;
  const Digraph::NodeMap<double> &pot;
  
public:
  Value operator[](Key e) const {
    return orig_len[e]-(pot[g.target(e)]-pot[g.source(e)]);
  }
  
  ReducedLengthMap(const Digraph &_g,
                   const Digraph::ArcMap &_o,
                   const Digraph::NodeMap &_p)
    : g(_g), orig_len(_o), pot(_p) {};
};

Then, you can call e.g. Dijkstra algoritm on this map like this:

...
ReducedLengthMap rm(g,len,pot);
Dijkstra<Digraph,ReducedLengthMap> dij(g,rm);
dij.run(s);
...

7.1 Map Concepts

...

7.2 Creating Own Maps

...

7.3 Map Adaptors

See Map Adaptors in the reference manual.

7.4 Using Algorithms with Special Maps

The basic functionality of the algorithms can be highly extended using special purpose map types for their internal data structures. For example, the Dijkstra class stores a ef ProcessedMap, which has to be a writable node map of bool value type. The assigned value of each node is set to true when the node is processed, i.e., its actual distance is found. Applying a special map, LoggerBoolMap, the processed order of the nodes can easily be stored in a standard container.

Such specific map types can be passed to the algorithms using the technique of named template parameters. Similarly to the named function parameters, they allow specifying any subset of the parameters and in arbitrary order.

Let us suppose that we have a traffic network stored in a LEMON digraph structure with two arc maps length and speed, which denote the physical length of each arc and the maximum (or average) speed that can be achieved on the corresponding road-section, respectively. If we are interested in the best traveling times, the following code can be used.

dijkstra(g, divMap(length, speed)).distMap(dist).run(s);

typedef vector<ListDigraph::Node> Container;
typedef back_insert_iterator<Container> InsertIterator;
typedef LoggerBoolMap<InsertIterator> ProcessedMap;
Dijkstra<ListDigraph>
  ::SetProcessedMap<ProcessedMap>
  ::Create dijktra(g, length);

Container container;
InsertIterator iterator(container);
ProcessedMap processed(iterator);

dijkstra.processedMap(processed).run(s);

The function-type interfaces are considerably simpler, but they can be used in almost all practical cases. Surprisingly, even the above example can also be implemented using the dijkstra() function and named parameters, as follows. Note that the function-type interface has the major advantage that temporary objects can be passed as parameters.

vector<ListDigraph::Node> process_order;
dijkstra(g, length)
  .processedMap(loggerBoolMap(back_inserter(process_order)))
  .run(s);

Let us see a bit more complex example to demonstrate Dfs's capabilities.

We will see a program, which solves the problem of topological ordering. We need to know in which order we should put on our clothes. The program will do the following:

1. We run the dfs algorithm to all nodes.
2. Put every node into a list when processed completely.
3. Write out the list in reverse order.

First of all we will need an own ProcessedMap. The ordering will be done through it.

The class meets the WriteMap concept. In it's set() method the only thing we need to do is insert the key - that is the node whose processing just finished - into the beginning of the list.
Although we implemented this needed helper class ourselves it was not necessary. The FrontInserterBoolMap class does exactly what we needed. To be correct it's more general - and it's all in LEMON. But we wanted to show you, how easy is to add additional functionality.

First we declare the needed data structures: the digraph and a map to store the nodes' label.

Now we build a digraph. But keep in mind that it must be DAG because cyclic digraphs has no topological ordering.

We label them...

Then add arcs which represent the precedences between those items.

See how easy is to access the internal information of this algorithm trough maps. We only need to set our own map as the class's ProcessedMap.

And now comes the third part. Write out the list in reverse order. But the list was composed in reverse way (with push_front() instead of push_back() so we just iterate it.

The program is to be found in the demo directory: topological_ordering.cc

LEMON also contains visitor based algorithm classes for BFS and DFS.

Skeleton visitor classes are defined for both BFS and DFS, the concrete implementations can be inherited from them.

template <typename GR>
struct DfsVisitor {
  void start(const typename GR::Node& node) {}
  void stop(const typename GR::Node& node) {}
  void reach(const typename GR::Node& node) {}
  void leave(const typename GR::Node& node) {}
  void discover(const typename GR::Arc& arc) {}
  void examine(const typename GR::Arc& arc) {}
  void backtrack(const typename GR::Arc& arc) {}
};

In the following example, the discover()} and

 {examine()
events are processed and the DFS tree is stored in an arc map.
The values of this map indicate whether the corresponding arc
reaches a new node or its target node is already reached.
\code
  template <typename GR>
  struct TreeVisitor : public DfsVisitor<GR> {
    TreeVisitor(typename GR::ArcMap<bool>& tree)
      : _tree(tree) {}
    void discover(const typename GR::Arc& arc)
      { _tree[arc] = true; }
    void examine(const typename GR::Arc& arc)
      { _tree[arc] = false; }
    typename GR::ArcMap<bool>& _tree;
  };

<< 6 Basic Graph Utilities | Home | 8 Graph Structures >>