Detailed Description

template<typename GR, typename WM>
class lemon::MaxWeightedPerfectFractionalMatching< GR, WM >

This class provides an efficient implementation of fractional matching algorithm. The implementation uses priority queues and provides 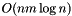$O(nm\log n)$ time complexity.

The maximum weighted fractional perfect matching is a relaxation of the maximum weighted perfect matching problem where the odd set constraints are omitted. It can be formulated with the following linear program.

$\sum_{e \in \delta(u)}x_e = 1 \quad \forall u\in V$

$x_e \ge 0\quad \forall e\in E$

$\max \sum_{e\in E}x_ew_e$

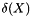where $\delta(X)$ is the set of edges incident to a node in 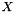$X$ . The result must be the union of a matching with one value edges and a set of odd length cycles with half value edges.

The algorithm calculates an optimal fractional matching and a proof of the optimality. The solution of the dual problem can be used to check the result of the algorithm. The dual linear problem is the following.

$y_u + y_v \ge w_{uv} \quad \forall uv\in E$

$\min \sum_{u \in V}y_u$

The algorithm can be executed with the run() function. After it the matching (the primal solution) and the dual solution can be obtained using the query functions.

The primal solution is multiplied by 2. If the value type is integer, then the dual solution is scaled by 4.

Template Parameters

GR	The undirected graph type the algorithm runs on.
WM	The type edge weight map. The default type is GR::EdgeMap<int>.

#include <lemon/fractional_matching.h>

Public Types
typedef GR	Graph
	The graph type of the algorithm.

typedef WM	WeightMap
	The type of the edge weight map.

typedef WeightMap::Value	Value
	The value type of the edge weights.

typedef Graph::template NodeMap< typename Graph::Arc >	MatchingMap
	The type of the matching map.

Public Member Functions
	MaxWeightedPerfectFractionalMatching (const Graph &graph, const WeightMap &weight, bool allow_loops=true)
	Constructor. More...

Execution Control
The simplest way to execute the algorithm is to use the run() member function.
void	init ()
	Initialize the algorithm. More...

bool	start ()
	Start the algorithm. More...

bool	run ()
	Run the algorithm. More...

Primal Solution
Functions to get the primal solution, i.e. the maximum weighted matching. Either run() or start() function should be called before using them.
Value	matchingWeight () const
	Return the weight of the matching. More...

int	matchingSize () const
	Return the number of covered nodes in the matching. More...

int	matching (const Edge &edge) const
	Return `true` if the given edge is in the matching. More...

Arc	matching (const Node &node) const
	Return the fractional matching arc (or edge) incident to the given node. More...

const MatchingMap &	matchingMap () const
	Return a const reference to the matching map. More...

Dual Solution
Functions to get the dual solution. Either run() or start() function should be called before using them.
Value	dualValue () const
	Return the value of the dual solution. More...

Value	nodeValue (const Node &n) const
	Return the dual value (potential) of the given node. More...

Static Public Attributes
static const int	primalScale = 2
	Scaling factor for primal solution. More...

static const int	dualScale
	Scaling factor for dual solution. More...

Constructor & Destructor Documentation

MaxWeightedPerfectFractionalMatching	(	const Graph &	graph,
		const WeightMap &	weight,
		bool	allow_loops = `true`
	)

inline

Constructor.

Member Function Documentation

void init ( )

inline

This function initializes the algorithm.

bool start ( )

inline

This function starts the algorithm.

Precondition: init() must be called before using this function.

bool run ( )

inline

This method runs the MaxWeightedPerfectFractionalMatching algorithm.

Note: mwfm.run() is just a shortcut of the following code.
* mwpfm.init();

* mwpfm.start();

*

Value matchingWeight ( ) const

inline

This function returns the weight of the found matching. This value is scaled by primal scale.

Precondition: Either run() or start() must be called before using this function.

int matchingSize ( ) const

inline

This function returns the number of covered nodes in the matching.

Precondition: Either run() or start() must be called before using this function.

int matching ( const Edge & edge ) const

inline

This function returns true if the given edge is in the found matching. The result is scaled by primal scale.

Precondition: Either run() or start() must be called before using this function.

Arc matching ( const Node & node ) const

inline

This function returns one of the fractional matching arc (or edge) incident to the given node in the found matching or INVALID if the node is not covered by the matching or if the node is on an odd length cycle then it is the successor edge on the cycle.

Precondition: Either run() or start() must be called before using this function.

const MatchingMap& matchingMap ( ) const

inline

This function returns a const reference to a node map that stores the matching arc (or edge) incident to each node.

Value dualValue ( ) const

inline

This function returns the value of the dual solution. It should be equal to the primal value scaled by dual scale.

Precondition: Either run() or start() must be called before using this function.

Value nodeValue ( const Node & n ) const

inline

This function returns the dual value (potential) of the given node.

Precondition: Either run() or start() must be called before using this function.

Member Data Documentation

const int primalScale = 2

static

Scaling factor for primal solution.

const int dualScale

static

Initial value:

=

std::numeric_limits<Value>::is_integer ? 4 : 1

Scaling factor for dual solution. It is equal to 4 or 1 according to the value type.

Detailed Description

template<typename GR, typename WM> class lemon::MaxWeightedPerfectFractionalMatching< GR, WM >

Public Types

Public Member Functions

Static Public Attributes

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation

template<typename GR, typename WM>
class lemon::MaxWeightedPerfectFractionalMatching< GR, WM >