Maximum Flow algorithms
[Algorithms]
Detailed Description
This group describes the algorithms for finding maximum flows and feasible circulations.
The maximum flow problem is to find a flow between a single source and a single target that is maximum. Formally, there is a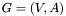 
directed graph, an 
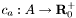capacity function and given 
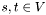source and target node. The maximum flow is the 
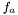solution of the next optimization problem:
![\[ 0 \le f_a \le c_a \]](form_83.png)
![\[ \sum_{v\in\delta^{-}(u)}f_{vu}=\sum_{v\in\delta^{+}(u)}f_{uv} \qquad \forall u \in V \setminus \{s,t\}\]](form_118.png)
![\[ \max \sum_{v\in\delta^{+}(s)}f_{uv} - \sum_{v\in\delta^{-}(s)}f_{vu}\]](form_85.png)
LEMON contains several algorithms for solving maximum flow problems:
- Edmonds-Karp
- Goldberg's Preflow algorithm
- Dinitz's blocking flow algorithm with dynamic trees
- Preflow algorithm with dynamic trees
In most cases the Preflow algorithm provides the fastest method to compute the maximum flow. All impelementations provides functions to query the minimum cut, which is the dual linear programming problem of the maximum flow.
Classes | |
| class | Circulation< _Graph, _LCapMap, _UCapMap, _DeltaMap, _Traits > |
| Push-relabel algorithm for the Network Circulation Problem. More... | |
| class | DinitzSleatorTarjan< _Graph, _CapacityMap, _Traits > |
| Dinitz-Sleator-Tarjan algorithms class. More... | |
| class | EdmondsKarp< _Graph, _CapacityMap, _Traits > |
| Edmonds-Karp algorithms class. More... | |
| class | GoldbergTarjan< _Graph, _CapacityMap, _Traits > |
| Goldberg-Tarjan algorithms class. More... | |
| class | Preflow< _Graph, _CapacityMap, _Traits > |
| Preflow algorithms class. More... | |
Files | |
| file | circulation.h |
| Push-prelabel algorithm for finding a feasible circulation. | |
| file | dinitz_sleator_tarjan.h |
| Implementation the dynamic tree data structure of Sleator and Tarjan. | |
| file | edmonds_karp.h |
| Implementation of the Edmonds-Karp algorithm. | |
| file | goldberg_tarjan.h |
| Implementation of the preflow algorithm. | |
| file | preflow.h |
| Implementation of the preflow algorithm. | |
