BellmanFord< _Graph, _LengthMap, _Traits > Class Template Reference
[Shortest Path algorithms]

Detailed Description

template<typename _Graph, typename _LengthMap, typename _Traits>
class lemon::BellmanFord< _Graph, _LengthMap, _Traits >

This class provides an efficient implementation of Bellman-Ford algorithm. The edge lengths are passed to the algorithm using a ReadMap, so it is easy to change it to any kind of length.

The Bellman-Ford algorithm solves the shortest path from one node problem when the edges can have negative length but the graph should not contain cycles with negative sum of length. If we can assume that all edge is non-negative in the graph then the dijkstra algorithm should be used rather.

The maximal time complexity of the algorithm is 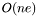$ O(ne) $ .

The type of the length is determined by the Value of the length map.

Parameters:

	_Graph	The graph type the algorithm runs on. The default value is ListGraph. The value of _Graph is not used directly by BellmanFord, it is only passed to BellmanFordDefaultTraits.
	_LengthMap	This read-only EdgeMap determines the lengths of the edges. The default map type is Graph::EdgeMap<int>. The value of _LengthMap is not used directly by BellmanFord, it is only passed to BellmanFordDefaultTraits.
	_Traits	Traits class to set various data types used by the algorithm. The default traits class is BellmanFordDefaultTraits<_Graph,_LengthMap>. See BellmanFordDefaultTraits for the documentation of a BellmanFord traits class.

Author:: Balazs Dezso

#include <lemon/bellman_ford.h>

List of all members.

Query Functions

The result of the BellmanFord algorithm can be obtained using these functions.
Before the use of these functions, either run() or start() must be called.

typedef PredMapPath< Graph,
PredMap > Path

Path path (Node t)

Gives back the shortest path.

Value dist (Node v) const

The distance of a node from the root.

Edge predEdge (Node v) const

Returns the 'previous edge' of the shortest path tree.

Node predNode (Node v) const

Returns the 'previous node' of the shortest path tree.

const DistMap & distMap () const

Returns a reference to the NodeMap of distances.

const PredMap & predMap () const

Returns a reference to the shortest path tree map.

bool reached (Node v)

Checks if a node is reachable from the root.

Classes

class ActiveIt

Lemon iterator for get the active nodes. More...

struct DefDistMap

struct DefOperationTraits

struct DefPredMap

Named parameter for setting PredMap type Named parameter for setting PredMap type More...

class UninitializedParameter

Exception for uninitialized parameters. More...

Public Types

typedef _Traits::Graph Graph

The type of the underlying graph.

typedef _Traits::LengthMap::Value Value

The type of the length of the edges.

typedef _Traits::LengthMap LengthMap

The type of the map that stores the edge lengths.

typedef _Traits::PredMap PredMap

The type of the map that stores the last edges of the shortest paths.

typedef _Traits::DistMap DistMap

The type of the map that stores the dists of the nodes.

typedef _Traits::OperationTraits OperationTraits

The operation traits.

Public Member Functions

BellmanFord (const Graph &_graph, const LengthMap &_length)

Constructor.

~BellmanFord ()

Destructor.

BellmanFord & lengthMap (const LengthMap &m)

Sets the length map.

BellmanFord & predMap (PredMap &m)

Sets the map storing the predecessor edges.

BellmanFord & distMap (DistMap &m)

Sets the map storing the distances calculated by the algorithm.

Execution control

The simplest way to execute the algorithm is to use one of the member functions called run(...).
If you need more control on the execution, first you must call init(), then you can add several source nodes with addSource(). Finally start() will perform the actual path computation.

void init (const Value value=OperationTraits::infinity())

void addSource (Node source, Value dst=OperationTraits::zero())

Adds a new source node.

bool processNextRound ()

Executes one round from the Bellman-Ford algorithm.

bool processNextWeakRound ()

Executes one weak round from the Bellman-Ford algorithm.

void start ()

Executes the algorithm.

bool checkedStart ()

Executes the algorithm and checks the negative cycles.

void limitedStart (int num)

Executes the algorithm with path length limit.

void run (Node s)

Runs BellmanFord algorithm from node s.

void run (Node s, int num)

Runs BellmanFord algorithm with limited path length from node s.

Private Member Functions

void create_maps ()

Creates the maps if necessary.

Private Attributes

const Graph * graph

Pointer to the underlying graph.

const LengthMap * length

Pointer to the length map.

PredMap * _pred

Pointer to the map of predecessors edges.

bool local_pred

Indicates if _pred is locally allocated (true) or not.

DistMap * _dist

Pointer to the map of distances.

bool local_dist

Indicates if _dist is locally allocated (true) or not.

Constructor & Destructor Documentation

BellmanFord	(	const Graph &	_graph,
		const LengthMap &	_length
	)			`[inline]`

Parameters:

	_graph	the graph the algorithm will run on.
	_length	the length map used by the algorithm.

Member Function Documentation

BellmanFord& lengthMap ( const LengthMap & m ) [inline]

Sets the length map.

Returns:: (*this)

BellmanFord& predMap ( PredMap & m ) [inline]

Sets the map storing the predecessor edges. If you don't use this function before calling run(), it will allocate one. The destuctor deallocates this automatically allocated map, of course.

Returns:: (*this)

BellmanFord& distMap ( DistMap & m ) [inline]

Sets the map storing the distances calculated by the algorithm. If you don't use this function before calling run(), it will allocate one. The destuctor deallocates this automatically allocated map, of course.

Returns:: (*this)

void init ( const Value value = OperationTraits::infinity() ) [inline]

Initializes the internal data structures.

void addSource	(	Node	source,
		Value	dst = `OperationTraits::zero()`
	)			`[inline]`

Adds a new source node. The optional second parameter is the initial distance of the node. It just sets the distance of the node to the given value.

bool processNextRound ( ) [inline]

If the algoritm calculated the distances in the previous round exactly for all at most 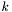$ k $ length path lengths then it will calculate the distances exactly for all at most 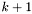$ k + 1 $ length path lengths. With 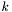$ k $ iteration this function calculates the at most 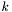$ k $ length path lengths.

Warning:: The paths with limited edge number cannot be retrieved easily with path() or predEdge() functions. If you need the shortest path and not just the distance you should store after each iteration the predMap() map and manually build the path.

Returns:: true when the algorithm have not found more shorter paths.

bool processNextWeakRound ( ) [inline]

If the algorithm calculated the distances in the previous round at least for all at most k length paths then it will calculate the distances at least for all at most k + 1 length paths. This function does not make it possible to calculate strictly the at most k length minimal paths, this is why it is called just weak round.

Returns:: true when the algorithm have not found more shorter paths.

void start ( ) [inline]

Precondition:: init() must be called and at least one node should be added with addSource() before using this function.

This method runs the BellmanFord algorithm from the root node(s) in order to compute the shortest path to each node. The algorithm computes

The shortest path tree.
The distance of each node from the root(s).

bool checkedStart ( ) [inline]

Precondition:: init() must be called and at least one node should be added with addSource() before using this function.

This method runs the BellmanFord algorithm from the root node(s) in order to compute the shortest path to each node. The algorithm computes

The shortest path tree.
The distance of each node from the root(s).

Returns:: false if there is a negative cycle in the graph.

void limitedStart ( int num ) [inline]

Precondition:: init() must be called and at least one node should be added with addSource() before using this function.

This method runs the BellmanFord algorithm from the root node(s) in order to compute the shortest path lengths with at most num edge.

Warning:: The paths with limited edge number cannot be retrieved easily with path() or predEdge() functions. If you need the shortest path and not just the distance you should store after each iteration the predMap() map and manually build the path.

The algorithm computes

The predecessor edge from each node.
The limited distance of each node from the root(s).

void run ( Node s ) [inline]

This method runs the BellmanFord algorithm from a root node s in order to compute the shortest path to each node. The algorithm computes

The shortest path tree.
The distance of each node from the root.

Note:

d.run(s) is just a shortcut of the following code.

         d.init();
         d.addSource(s);
         d.start();

void run	(	Node	s,
		int	num
	)			`[inline]`

This method runs the BellmanFord algorithm from a root node s in order to compute the shortest path with at most len edges to each node. The algorithm computes

The shortest path tree.
The distance of each node from the root.

Note:

d.run(s, num) is just a shortcut of the following code.

         d.init();
         d.addSource(s);
         d.limitedStart(num);

Path path ( Node t ) [inline]

Gives back the shortest path.

Precondition:: The t should be reachable from the source.

Value dist ( Node v ) const [inline]

Returns the distance of a node from the root.

Precondition:: run() must be called before using this function.

Warning:: If node v in unreachable from the root the return value of this funcion is undefined.

Edge predEdge ( Node v ) const [inline]

For a node v it returns the 'previous edge' of the shortest path tree, i.e. it returns the last edge of a shortest path from the root to v. It is INVALID if v is unreachable from the root or if v=s. The shortest path tree used here is equal to the shortest path tree used in predNode().

Precondition:: run() must be called before using this function.

Node predNode ( Node v ) const [inline]

For a node v it returns the 'previous node' of the shortest path tree, i.e. it returns the last but one node from a shortest path from the root to /v. It is INVALID if v is unreachable from the root or if v=s. The shortest path tree used here is equal to the shortest path tree used in predEdge().

Precondition:: run() must be called before using this function.

const DistMap& distMap ( ) const [inline]

Returns a reference to the NodeMap of distances.

Precondition:: run() must be called before using this function.

const PredMap& predMap ( ) const [inline]

Returns a reference to the NodeMap of the edges of the shortest path tree.

Precondition:: run() must be called before using this function.

bool reached ( Node v ) [inline]

Returns true if v is reachable from the root.

Precondition:: run() must be called before using this function.


Query Functions
The result of the BellmanFord algorithm can be obtained using these functions. Before the use of these functions, either run() or start() must be called.
typedef PredMapPath< Graph, PredMap >	Path
Path	path (Node t)
	Gives back the shortest path.
Value	dist (Node v) const
	The distance of a node from the root.
Edge	predEdge (Node v) const
	Returns the 'previous edge' of the shortest path tree.
Node	predNode (Node v) const
	Returns the 'previous node' of the shortest path tree.
const DistMap &	distMap () const
	Returns a reference to the NodeMap of distances.
const PredMap &	predMap () const
	Returns a reference to the shortest path tree map.
bool	reached (Node v)
	Checks if a node is reachable from the root.
Classes
class	ActiveIt
	Lemon iterator for get the active nodes. More...
struct	DefDistMap
struct	DefOperationTraits
struct	DefPredMap
	Named parameter for setting PredMap type Named parameter for setting PredMap type More...
class	UninitializedParameter
	Exception for uninitialized parameters. More...
Public Types
typedef _Traits::Graph	Graph
	The type of the underlying graph.
typedef _Traits::LengthMap::Value	Value
	The type of the length of the edges.
typedef _Traits::LengthMap	LengthMap
	The type of the map that stores the edge lengths.
typedef _Traits::PredMap	PredMap
	The type of the map that stores the last edges of the shortest paths.
typedef _Traits::DistMap	DistMap
	The type of the map that stores the dists of the nodes.
typedef _Traits::OperationTraits	OperationTraits
	The operation traits.
Public Member Functions
	BellmanFord (const Graph &_graph, const LengthMap &_length)
	Constructor.
	~BellmanFord ()
	Destructor.
BellmanFord &	lengthMap (const LengthMap &m)
	Sets the length map.
BellmanFord &	predMap (PredMap &m)
	Sets the map storing the predecessor edges.
BellmanFord &	distMap (DistMap &m)
	Sets the map storing the distances calculated by the algorithm.
Execution control
The simplest way to execute the algorithm is to use one of the member functions called `run`(...). If you need more control on the execution, first you must call init(), then you can add several source nodes with addSource(). Finally start() will perform the actual path computation.
void	init (const Value value=OperationTraits::infinity())
void	addSource (Node source, Value dst=OperationTraits::zero())
	Adds a new source node.
bool	processNextRound ()
	Executes one round from the Bellman-Ford algorithm.
bool	processNextWeakRound ()
	Executes one weak round from the Bellman-Ford algorithm.
void	start ()
	Executes the algorithm.
bool	checkedStart ()
	Executes the algorithm and checks the negative cycles.
void	limitedStart (int num)
	Executes the algorithm with path length limit.
void	run (Node s)
	Runs BellmanFord algorithm from node `s`.
void	run (Node s, int num)
	Runs BellmanFord algorithm with limited path length from node `s`.
Private Member Functions
void	create_maps ()
	Creates the maps if necessary.
Private Attributes
const Graph *	graph
	Pointer to the underlying graph.
const LengthMap *	length
	Pointer to the length map.
PredMap *	_pred
	Pointer to the map of predecessors edges.
bool	local_pred
	Indicates if _pred is locally allocated (`true`) or not.
DistMap *	_dist
	Pointer to the map of distances.
bool	local_dist
	Indicates if _dist is locally allocated (`true`) or not.

BellmanFord< _Graph, _LengthMap, _Traits > Class Template Reference [Shortest Path algorithms]

Detailed Description

template<typename _Graph, typename _LengthMap, typename _Traits> class lemon::BellmanFord< _Graph, _LengthMap, _Traits >

Query Functions

Classes

Public Types

Public Member Functions

Private Member Functions

Private Attributes

Constructor & Destructor Documentation

Member Function Documentation

BellmanFord< _Graph, _LengthMap, _Traits > Class Template Reference
[Shortest Path algorithms]

template<typename _Graph, typename _LengthMap, typename _Traits>
class lemon::BellmanFord< _Graph, _LengthMap, _Traits >