EdgeSubGraphAdaptor< Graph, EdgeFilterMap > Class Template Reference
[Adaptor Classes for Graphs]

---

Detailed Description

template<typename Graph, typename EdgeFilterMap>
class lemon::EdgeSubGraphAdaptor< Graph, EdgeFilterMap >

An adaptor for hiding edges from a graph. This adaptor specializes SubGraphAdaptor in the way that only the edge-set can be filtered. The usefulness of this adaptor is demonstrated in the problem of searching a maximum number of edge-disjoint shortest paths between two nodes s and t. Shortest here means being shortest w.r.t. non-negative edge-lengths. Note that the comprehension of the presented solution need's some elementary knowledge from combinatorial optimization.

If a single shortest path is to be searched between s and t, then this can be done easily by applying the Dijkstra algorithm. What happens, if a maximum number of edge-disjoint shortest paths is to be computed. It can be proved that an edge can be in a shortest path if and only if it is tight with respect to the potential function computed by Dijkstra. Moreover, any path containing only such edges is a shortest one. Thus we have to compute a maximum number of edge-disjoint paths between s and t in the graph which has edge-set all the tight edges. The computation will be demonstrated on the following graph, which is read from the dimacs file sub_graph_adaptor_demo.dim. The full source code is available in sub_graph_adaptor_demo.cc. If you are interested in more demo programs, you can use dim_to_dot.cc to generate .dot files from dimacs files. The .dot file of the following figure was generated by the demo program dim_to_dot.cc.

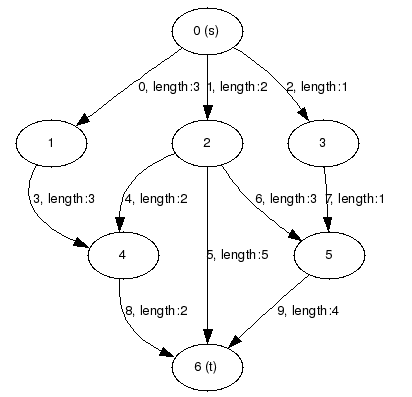
     Graph g;
     Node s, t;
     LengthMap length(g);
     
     readDimacs(std::cin, g, length, s, t);
     
     cout << "edges with lengths (of form id, source--length->target): " << endl;
     for(EdgeIt e(g); e!=INVALID; ++e) 
       cout << g.id(e) << ", " << g.id(g.source(e)) << "--" 
            << length[e] << "->" << g.id(g.target(e)) << endl;
     
     cout << "s: " << g.id(s) << " t: " << g.id(t) << endl;

Next, the potential function is computed with Dijkstra.

     typedef Dijkstra<Graph, LengthMap> Dijkstra;
     Dijkstra dijkstra(g, length);
     dijkstra.run(s);

Next, we consrtruct a map which filters the edge-set to the tight edges.

     typedef TightEdgeFilterMap<Graph, const Dijkstra::DistMap, LengthMap> 
       TightEdgeFilter;
     TightEdgeFilter tight_edge_filter(g, dijkstra.distMap(), length);
     
     typedef EdgeSubGraphAdaptor<Graph, TightEdgeFilter> SubGA;
     SubGA ga(g, tight_edge_filter);

Then, the maximum nimber of edge-disjoint s-t paths are computed with a max flow algorithm Preflow.

     ConstMap<Edge, int> const_1_map(1);
     Graph::EdgeMap<int> flow(g, 0);
     
     Preflow<SubGA, ConstMap<Edge, int>, Graph::EdgeMap<int> > 
       preflow(ga, const_1_map, s, t);
     preflow.run();

Last, the output is:

     cout << "maximum number of edge-disjoint shortest path: " 
          << preflow.flowValue() << endl;
     cout << "edges of the maximum number of edge-disjoint shortest s-t paths: " 
          << endl;
     for(EdgeIt e(g); e!=INVALID; ++e) 
       if (preflow.flow(e))
         cout << " " << g.id(g.source(e)) << "--"
              << length[e] << "->" << g.id(g.target(e)) << endl;

The program has the following (expected :-)) output:

     edges with lengths (of form id, source--length->target):
      9, 5--4->6
      8, 4--2->6
      7, 3--1->5
      6, 2--3->5
      5, 2--5->6
      4, 2--2->4
      3, 1--3->4
      2, 0--1->3
      1, 0--2->2
      0, 0--3->1
     s: 0 t: 6
     maximum number of edge-disjoint shortest path: 2
     edges of the maximum number of edge-disjoint shortest s-t paths:
      9, 5--4->6
      8, 4--2->6
      7, 3--1->5
      4, 2--2->4
      2, 0--1->3
      1, 0--2->2

Author:

Marton Makai

#include <lemon/graph_adaptor.h>

Inheritance diagram for EdgeSubGraphAdaptor< Graph, EdgeFilterMap >:

[legend]

List of all members.