Suurballe< Graph, LengthMap > Class Template Reference
[Shortest Path algorithms]

---

Detailed Description

template<typename Graph, typename LengthMap = typename Graph::template EdgeMap<int>>
class lemon::Suurballe< Graph, LengthMap >

Suurballe implements an algorithm for finding edge-disjoint paths having minimum total length (cost) from a given source node to a given target node in a directed graph.

In fact, this implementation is the specialization of the successive shortest path algorithm.

Template Parameters:

	Graph	The directed graph type the algorithm runs on.
	LengthMap	The type of the length (cost) map.

Warning:

Length values should be non-negative integers.

Note:

For finding node-disjoint paths this algorithm can be used with SplitGraphAdaptor.

Author:

Attila Bernath and Peter Kovacs

#include <lemon/suurballe.h>

List of all members.

Classes
class	ResidualDijkstra
	Special implementation of the Dijkstra algorithm for finding shortest paths in the residual network. More...
Public Types
typedef Graph::template EdgeMap< int >	FlowMap
	The type of the flow map.
typedef Graph::template NodeMap< Length >	PotentialMap
	The type of the potential map.
typedef SimplePath< Graph >	Path
	The type of the path structures.
Public Member Functions
	Suurballe (const Graph &graph, const LengthMap &length, Node s, Node t)
	Constructor.
	~Suurballe ()
	Destructor.
Suurballe &	flowMap (FlowMap &map)
	Sets the flow map.
Suurballe &	potentialMap (PotentialMap &map)
	Sets the potential map.
Execution control
The simplest way to execute the algorithm is to call the run() function. If you only need the flow that is the union of the found edge-disjoint paths, you may call init() and findFlow().
int	run (int k=2)
	Runs the algorithm.
void	init ()
int	findFlow (int k=2)
	Executes the successive shortest path algorithm to find an optimal flow.
void	findPaths ()
	Computes the paths from the flow.
Query Functions
The result of the algorithm can be obtained using these functions. The algorithm should be executed before using them.
const FlowMap &	flowMap () const
	Returns a const reference to the edge map storing the found flow.
const PotentialMap &	potentialMap () const
	Returns a const reference to the node map storing the found potentials (the dual solution).
int	flow (const Edge &edge) const
	Returns the flow on the given edge.
Length	potential (const Node &node) const
	Returns the potential of the given node.
Length	totalLength () const
	Returns the total length (cost) of the found paths (flow).
int	pathNum () const
	Returns the number of the found paths.
Path	path (int i) const
	Returns a const reference to the specified path.

---

Constructor & Destructor Documentation

Suurballe	(	const Graph &	graph,
		const LengthMap &	length,
		Node	s,
		Node	t
	)			[inline]

Constructor.

Parameters:

	graph	The directed graph the algorithm runs on.
	length	The length (cost) values of the edges.
	s	The source node.
	t	The target node.

---

Member Function Documentation

Suurballe& flowMap

(

FlowMap &

map

)

[inline]

Sets the flow map.

The found flow contains only 0 and 1 values. It is the union of the found edge-disjoint paths.

Returns:

(*this)

Suurballe& potentialMap

(

PotentialMap &

map

)

[inline]

Sets the potential map.

The potentials provide the dual solution of the underlying minimum cost flow problem.

Returns:

(*this)

int run

(

int

k = 2

)

[inline]

Runs the algorithm.

Parameters:

k

The number of paths to be found.

Returns:

k if there are at least k edge-disjoint paths from s to t. Otherwise it returns the number of edge-disjoint paths found.

Note:

Apart from the return value, s.run(k) is just a shortcut of the following code.

   s.init();
   s.findFlow(k);
   s.findPaths();

void init

(

)

[inline]

Initializes the algorithm.

int findFlow

(

int

k = 2

)

[inline]

Executes the successive shortest path algorithm to find a minimum cost flow, which is the union of k or less edge-disjoint paths.

Returns:

k if there are at least k edge-disjoint paths from s to t. Otherwise it returns the number of edge-disjoint paths found.

Precondition:

init() must be called before using this function.

void findPaths

(

)

[inline]

Computes the paths from the flow.

Precondition:

init() and findFlow() must be called before using this function.

const FlowMap& flowMap

(

)

const [inline]

Returns a const reference to the edge map storing the flow that is the union of the found edge-disjoint paths.

Precondition:

run() or findFlow() must be called before using this function.

const PotentialMap& potentialMap

(

)

const [inline]

Returns a const reference to the node map storing the found potentials that provide the dual solution of the underlying minimum cost flow problem.

Precondition:

run() or findFlow() must be called before using this function.

int flow

(

const Edge &

edge

)

const [inline]

Returns the flow on the given edge. It is 1 if the edge is involved in one of the found paths, otherwise it is 0.

Precondition:

run() or findFlow() must be called before using this function.

Length potential

(

const Node &

node

)

const [inline]

Returns the potential of the given node.

Precondition:

run() or findFlow() must be called before using this function.

Length totalLength

(

)

const [inline]

Returns the total length (cost) of the found paths (flow). The complexity of the function is .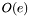

Precondition:

run() or findFlow() must be called before using this function.

int pathNum

(

)

const [inline]

Returns the number of the found paths.

Precondition:

run() or findFlow() must be called before using this function.

Path path

(

int

i

)

const [inline]

Returns a const reference to the specified path.

Parameters:

i

The function returns the i-th path. i must be between 0 and pathNum()-1.

Precondition:

run() or findPaths() must be called before using this function.