Minimum Cut algorithms
[Algorithms]
Detailed Description
This group describes the algorithms for finding minimum cut in graphs.
The minimum cut problem is to find a non-empty and non-complete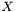 
subset of the vertices with minimum overall capacity on outgoing arcs. Formally, there is 
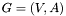directed graph, an 
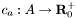capacity function. The minimum cut is the 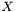solution of the next optimization problem:
![\[ \min_{X \subset V, X\not\in \{\emptyset, V\}}\sum_{uv\in A, u\in X, v\not\in X}c_{uv}\]](form_99.png)
LEMON contains several algorithms related to minimum cut problems:
- Hao-Orlin algorithm to calculate minimum cut in directed graphs
- Nagamochi-Ibaraki algorithm to calculate minimum cut in undirected graphs
- Gomory-Hu tree computation to calculate all pairs minimum cut in undirected graphs
If you want to find minimum cut just between two distinict nodes, please see the Maximum Flow page.
Classes | |
| class | GomoryHuTree< _UGraph, _Capacity > |
| Gomory-Hu cut tree algorithm. More... | |
| class | HaoOrlin< _Graph, _CapacityMap, _Tolerance > |
| Hao-Orlin algorithm to find a minimum cut in directed graphs. More... | |
| class | NagamochiIbaraki< _Graph, _CapacityMap, _Traits > |
| Calculates the minimum cut in an undirected graph. More... | |
Files | |
| file | gomory_hu_tree.h |
| Gomory-Hu cut tree in undirected graphs. | |
| file | hao_orlin.h |
| Implementation of the Hao-Orlin algorithm. | |
| file | nagamochi_ibaraki.h |
| Maximum cardinality search and minimum cut in undirected graphs. | |
