MaxBipartiteMatching< BpUGraph > Class Template Reference
[Matching algorithms]

---

Detailed Description

template<typename BpUGraph>
class lemon::MaxBipartiteMatching< BpUGraph >

Bipartite Max Cardinality Matching algorithm. This class implements the Hopcroft-Karp algorithm which has 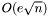time complexity.

Note:

In several cases the push-relabel based algorithms have better runtime performance than the augmenting path based ones.

See also:

PrBipartiteMatching

#include <lemon/bipartite_matching.h>

List of all members.

Execution control
The simplest way to execute the algorithm is to use one of the member functions called run(). If you need more control on the execution, first you must call init() or one alternative for it. Finally start() will perform the matching computation or with step-by-step execution you can augment the solution.
void	init ()
	Initalize the data structures.
void	greedyInit ()
	Initalize the data structures.
template<typename MatchingMap >
void	matchingInit (const MatchingMap &mm)
	Initalize the data structures with an initial matching.
template<typename MatchingMap >
bool	checkedMatchingInit (const MatchingMap &mm)
	Initalize the data structures with an initial matching.
bool	augment ()
	An augmenting phase of the Hopcroft-Karp algorithm.
bool	simpleAugment ()
	An augmenting phase with single path augementing.
void	start ()
	Starts the algorithm.
void	run ()
	Runs the algorithm.
bool	_find_path (Node anode, int maxlevel, typename Graph::template BNodeMap< int > &level)
void	_find_path_bfs (Node anode, typename Graph::template ANodeMap< UEdge > &pred)
Public Member Functions
	MaxBipartiteMatching (const BpUGraph &graph)
	Constructor.
Query Functions
The result of the Matching algorithm can be obtained using these functions. Before the use of these functions, either run() or start() must be called.
bool	matchingEdge (const UEdge &edge) const
	Return true if the given uedge is in the matching.
UEdge	matchingEdge (const Node &node) const
	Returns the matching edge from the node.
template<typename MatchingMap >
int	quickMatching (MatchingMap &mm) const
	Set true all matching uedge in the map.
template<typename MatchingMap >
int	matching (MatchingMap &mm) const
	Set true all matching uedge in the map and the others to false.
template<class MatchingMap >
int	aMatching (MatchingMap &mm) const
	Gives back the matching in an ANodeMap.
template<class MatchingMap >
int	bMatching (MatchingMap &mm) const
	Gives back the matching in a BNodeMap.
template<typename CoverMap >
int	coverSet (CoverMap &covering) const
	Returns a minimum covering of the nodes.
template<typename BarrierMap >
void	aBarrier (BarrierMap &barrier) const
	Gives back a barrier on the A-nodes.
template<typename BarrierMap >
void	bBarrier (BarrierMap &barrier) const
	Gives back a barrier on the B-nodes.
int	matchingSize () const

---

Constructor & Destructor Documentation

MaxBipartiteMatching

(

const BpUGraph &

graph

)

[inline]

Constructor of the algorithm.

---

Member Function Documentation

void init

(

)

[inline]

It initalizes the data structures and creates an empty matching.

void greedyInit

(

)

[inline]

It initalizes the data structures and creates a greedy matching. From this matching sometimes it is faster to get the matching than from the initial empty matching.

void matchingInit

(

const MatchingMap &

mm

)

[inline]

It initalizes the data structures with an initial matching.

bool checkedMatchingInit

(

const MatchingMap &

mm

)

[inline]

It initalizes the data structures with an initial matching.

Returns:

True when the given map contains really a matching.

bool augment

(

)

[inline]

It runs an augmenting phase of the Hopcroft-Karp algorithm. This phase finds maximal edge disjoint augmenting paths and augments on these paths. The algorithm consists at most of 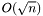phase and one phase is 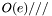long.

bool simpleAugment

(

)

[inline]

This phase finds only one augmenting paths and augments on these paths. The algorithm consists at most of 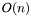phase and one phase is 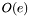long.

void start

(

)

[inline]

Starts the algorithm. It runs augmenting phases until the optimal solution reached.

void run

(

)

[inline]

It just initalize the algorithm and then start it.

bool matchingEdge

(

const UEdge &

edge

)

const [inline]

It returns true if the given uedge is in the matching.

UEdge matchingEdge

(

const Node &

node

)

const [inline]

Returns the matching edge from the node. If there is not such edge it gives back INVALID.

Note:

If the parameter node is a B-node then the running time is propotional to the degree of the node.

int quickMatching

(

MatchingMap &

mm

)

const [inline]

Set true all matching uedge in the map. It does not change the value mapped to the other uedges.

Returns:

The number of the matching edges.

int matching

(

MatchingMap &

mm

)

const [inline]

Set true all matching uedge in the map and the others to false.

Returns:

The number of the matching edges.

int aMatching

(

MatchingMap &

mm

)

const [inline]

Gives back the matching in an ANodeMap. The parameter should be a write ANodeMap of UEdge values.

Returns:

The number of the matching edges.

int bMatching

(

MatchingMap &

mm

)

const [inline]

Gives back the matching in a BNodeMap. The parameter should be a write BNodeMap of UEdge values.

Returns:

The number of the matching edges.

int coverSet

(

CoverMap &

covering

)

const [inline]

The minimum covering set problem is the dual solution of the maximum bipartite matching. It provides a solution for this problem what is proof of the optimality of the matching.

Returns:

The size of the cover set.

void aBarrier

(

BarrierMap &

barrier

)

const [inline]

The barrier is s subset of the nodes on the same side of the graph, which size minus its neighbours is exactly the unmatched nodes on the A-side.

Return values:

barrier

A WriteMap on the ANodes with bool value.

void bBarrier

(

BarrierMap &

barrier

)

const [inline]

The barrier is s subset of the nodes on the same side of the graph, which size minus its neighbours is exactly the unmatched nodes on the B-side.

Return values:

barrier

A WriteMap on the BNodes with bool value.

int matchingSize

(

)

const [inline]

Gives back the number of the matching edges.