MaxWeightedMatching< _UGraph, _WeightMap > Class Template Reference
[Matching algorithms]
Detailed Description
template<typename _UGraph, typename _WeightMap = typename _UGraph::template UEdgeMap<int>>
class lemon::MaxWeightedMatching< _UGraph, _WeightMap >
This class provides an efficient implementation of Edmond's maximum weighted matching algorithm. The implementation is based on extensive use of priority queues and provides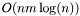 
time complexity.The maximum weighted matching problem is to find undirected edges in the graph with maximum overall weight and no two of them shares their endpoints. The problem can be formulated with the next linear program:
![\[ \sum_{e \in \delta(u)}x_e \le 1 \quad \forall u\in V\]](form_105.png)
![\[ \sum_{e \in \gamma(B)}x_e \le \frac{\vert B \vert - 1}{2} \quad \forall B\in\mathcal{O}\]](form_106.png)
![\[x_e \ge 0\quad \forall e\in E\]](form_107.png)
![\[\max \sum_{e\in E}x_ew_e\]](form_108.png)
where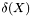 
is the set of edges incident to a node in 
, 
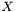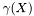is the set of edges with both endpoints in 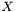and 
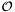is the set of odd cardinality subsets of the nodes.
The algorithm calculates an optimal matching and a proof of the optimality. The solution of the dual problem can be used to check the result of the algorithm. The dual linear problem is the next:
![\[ y_u + y_v + \sum_{B \in \mathcal{O}, uv \in \gamma(B)}z_B \ge w_{uv} \quad \forall uv\in E\]](form_112.png)
![\[y_u \ge 0 \quad \forall u \in V\]](form_113.png)
![\[z_B \ge 0 \quad \forall B \in \mathcal{O}\]](form_114.png)
![\[\min \sum_{u \in V}y_u + \sum_{B \in \mathcal{O}}\frac{\vert B \vert - 1}{2}z_B\]](form_115.png)
The algorithm can be executed with run() or the init() and then the start() member functions. After it the matching can be asked with matching() or mate() functions. The dual solution can be get with nodeValue(), blossomNum() and blossomValue() members and BlossomIt nested class which is able to iterate on the nodes of a blossom. If the value type is integral then the dual solution is multiplied by 4.
#include <lemon/max_matching.h>
Classes | |
| class | BlossomIt |
| Lemon iterator for get the items of the blossom. More... | |
Public Member Functions | |
| MaxWeightedMatching (const UGraph &ugraph, const WeightMap &weight) | |
Execution control | |
| void | init () |
| Initialize the algorithm. | |
| void | start () |
| Starts the algorithm. | |
| void | run () |
| Runs MaxWeightedMatching algorithm. | |
Primal solution | |
Functions for get the primal solution, ie. the matching. | |
| Value | matchingValue () const |
| bool | matching (const UEdge &edge) const |
| Edge | matching (const Node &node) const |
| Returns the incident matching edge. | |
| Node | mate (const Node &node) const |
| Returns the mate of the node. | |
Dual solution | |
Functions for get the dual solution. | |
| Value | dualValue () const |
| Returns the value of the dual solution. | |
| Value | nodeValue (const Node &n) const |
| Returns the value of the node. | |
| int | blossomNum () const |
| Returns the number of the blossoms in the basis. | |
| int | blossomSize (int k) const |
| Value | blossomValue (int k) const |
| Returns the value of the blossom. | |
Static Public Attributes | |
| static const int | dualScale |
| Scaling factor for dual solution. | |
Constructor & Destructor Documentation
| MaxWeightedMatching | ( | const UGraph & | ugraph, | |
| const WeightMap & | weight | |||
| ) | [inline] |
Constructor.
Member Function Documentation
| void init | ( | ) | [inline] |
Initialize the algorithm
| void start | ( | ) | [inline] |
Starts the algorithm
| void run | ( | ) | [inline] |
This method runs the MaxWeightedMatching algorithm.
- Note:
- mwm.run() is just a shortcut of the following code.
mwm.init(); mwm.start();
| Value matchingValue | ( | ) | const [inline] |
Returns the matching value.
| bool matching | ( | const UEdge & | edge | ) | const [inline] |
Returns true when the edge is in the matching.
| Edge matching | ( | const Node & | node | ) | const [inline] |
Returns the incident matching edge from given node. If the node is not matched then it gives back INVALID.
| Node mate | ( | const Node & | node | ) | const [inline] |
Returns the adjancent node in a mathcing edge. If the node is not matched then it gives back INVALID.
| Value dualValue | ( | ) | const [inline] |
Returns the value of the dual solution. It should be equal to the primal value scaled by dual scale.
| Value nodeValue | ( | const Node & | n | ) | const [inline] |
Returns the the value of the node.
| int blossomNum | ( | ) | const [inline] |
Returns the number of the blossoms in the basis.
- See also:
- BlossomIt
| int blossomSize | ( | int | k | ) | const [inline] |
Returns the number of the nodes in the blossom.
| Value blossomValue | ( | int | k | ) | const [inline] |
Returns the the value of the blossom.
- See also:
- BlossomIt
Member Data Documentation
const int dualScale [static] |
Initial value:
std::numeric_limits<Value>::is_integer ? 4 : 1
