MinCostMaxBipartiteMatching< _BpUGraph, _CostMap, _Traits > Class Template Reference
[Matching algorithms]

---

Detailed Description

template<typename _BpUGraph, typename _CostMap, typename _Traits>
class lemon::MinCostMaxBipartiteMatching< _BpUGraph, _CostMap, _Traits >

This class implements the bipartite Min Cost Matching algorithm. It uses the successive shortest path algorithm to calculate the minimum cost maximum matching in the bipartite graph. The time complexity of the algorithm is 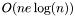with the default binary heap implementation but this can be improved to 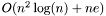if we use fibonacci heaps.

The algorithm also provides a potential function on the nodes which a dual solution of the matching algorithm and it can be used to proof the optimality of the given pimal solution. #include <lemon/bipartite_matching.h>

List of all members.

Classes
struct	DefHeap
struct	DefStandardHeap
	Named parameter for setting heap and cross reference type with automatic allocation More...
class	UninitializedParameter
	Exception for uninitialized parameters. More...
Public Member Functions
	MinCostMaxBipartiteMatching (const BpUGraph &_graph, const CostMap &_cost)
	Constructor.
	~MinCostMaxBipartiteMatching ()
	Destructor.
MinCostMaxBipartiteMatching &	heap (Heap &hp, HeapCrossRef &cr)
	Sets the heap and the cross reference used by algorithm.
Execution control
The simplest way to execute the algorithm is to use one of the member functions called run(). If you need more control on the execution, first you must call init() or one alternative for it. Finally start() will perform the matching computation or with step-by-step execution you can augment the solution.
void	init ()
	Initalize the data structures.
bool	augment ()
	An augmenting phase of the costed matching algorithm.
void	start ()
	Starts the algorithm.
void	run ()
	Runs the algorithm.
Query Functions
The result of the Matching algorithm can be obtained using these functions. Before the use of these functions, either run() or start() must be called.
template<typename PotentialMap >
void	potential (PotentialMap &pt) const
	Gives back the potential in the NodeMap.
template<typename MatchingMap >
int	quickMatching (MatchingMap &mm) const
	Set true all matching uedge in the map.
template<typename MatchingMap >
int	matching (MatchingMap &mm) const
	Set true all matching uedge in the map and the others to false.
template<class MatchingMap >
int	aMatching (MatchingMap &mm) const
	Gives back the matching in an ANodeMap.
template<class MatchingMap >
int	bMatching (MatchingMap &mm) const
	Gives back the matching in a BNodeMap.
bool	matchingEdge (const UEdge &edge) const
	Return true if the given uedge is in the matching.
UEdge	matchingEdge (const Node &node) const
	Returns the matching edge from the node.
Value	matchingCost () const
int	matchingSize () const

---

Constructor & Destructor Documentation

MinCostMaxBipartiteMatching	(	const BpUGraph &	_graph,
		const CostMap &	_cost
	)			[inline]

Constructor of the algorithm.

~MinCostMaxBipartiteMatching

(

)

[inline]

Destructor of the algorithm.

---

Member Function Documentation

MinCostMaxBipartiteMatching& heap	(	Heap &	hp,
		HeapCrossRef &	cr
	)			[inline]

Sets the heap and the cross reference used by algorithm. If you don't use this function before calling run(), it will allocate one. The destuctor deallocates this automatically allocated map, of course.

Returns:

(*this)

void init

(

)

[inline]

It initalizes the data structures and creates an empty matching.

bool augment

(

)

[inline]

It runs an augmenting phase of the matching algorithm. The phase finds the best augmenting path and augments only on this paths.

The algorithm consists at most of 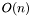phase and one phase is 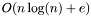long with Fibonacci heap or 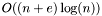long with binary heap.

void start

(

)

[inline]

Starts the algorithm. It runs augmenting phases until the optimal solution reached.

void run

(

)

[inline]

It just initalize the algorithm and then start it.

void potential

(

PotentialMap &

pt

)

const [inline]

Gives back the potential in the NodeMap. The matching is optimal with the current number of edges if 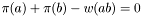for each matching edges and 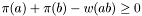for each edges.

int quickMatching

(

MatchingMap &

mm

)

const [inline]

Set true all matching uedge in the map. It does not change the value mapped to the other uedges.

Returns:

The number of the matching edges.

int matching

(

MatchingMap &

mm

)

const [inline]

Set true all matching uedge in the map and the others to false.

Returns:

The number of the matching edges.

int aMatching

(

MatchingMap &

mm

)

const [inline]

Gives back the matching in an ANodeMap. The parameter should be a write ANodeMap of UEdge values.

Returns:

The number of the matching edges.

int bMatching

(

MatchingMap &

mm

)

const [inline]

Gives back the matching in a BNodeMap. The parameter should be a write BNodeMap of UEdge values.

Returns:

The number of the matching edges.

bool matchingEdge

(

const UEdge &

edge

)

const [inline]

It returns true if the given uedge is in the matching.

UEdge matchingEdge

(

const Node &

node

)

const [inline]

Returns the matching edge from the node. If there is not such edge it gives back INVALID.

Value matchingCost

(

)

const [inline]

Gives back the sum of costs of the matching edges.

int matchingSize

(

)

const [inline]

Gives back the number of the matching edges.